[ 문제 ]
[ 문제 이해 ]
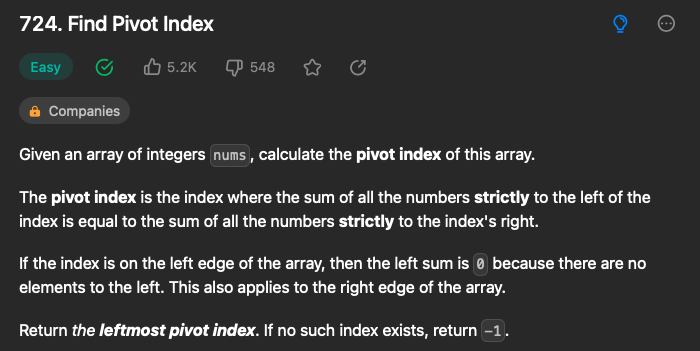
Int Array 가 주어졌을 때, Left sum과 Right sum이 같아지는 index를 리턴하고, 아니면 -1을 리턴해라.
[ 내가 푼 방식 ]
public int pivotIndex(int[] nums) {
for( int i = 0; i < nums.length; i++){
int lSum = 0;
int rSum = 0;
for( int j = 0; j < i ; j++){
lSum += nums[j];
}
for( int k = i+1 ; k < nums.length; k++){
rSum += nums[k];
}
if ( lSum == rSum ){
return i;
}
}
return -1;
}- Time Complexity: BigO(N^2)
- 그냥 보는 것 그대로 인덱스 i마다 왼/오 합을 전부 다 구해서 같으면 리턴함
- 풀면서도 이게 별로라는 것을 깨달았지만 다른 방법이 딱히 생각나지 않았음;
[ 정답 분석 ]
Find Pivot Index - LeetCode Discuss
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
Intuition and Algorithm
We need to quickly compute the sum of values to the left and the right of every index.
Let's say we knew S as the sum of the numbers, and we are at index i.
주어진 수들의 모든 합을 알고, 우리는 i 인덱스에 있다고 가정해보자.
If we knew the sum of numbers leftsum that are to the left of index i,
i 왼쪽에 있는 수들의 합을 모두 알고 있다면,
then the other sum to the right of the index would just be S - nums[i] - leftsum.
오른쪽 수들의 합은 전체 합 - 인덱스 - 왼쪽 합이 될 것이다.
As such, we only need to know about leftsum to check whether an index is a pivot index in constant time.
따라서, 우리는 왼쪽 합만 알고 있으면 인덱스가 피봇 인덱스인지 알 수 있다.
Let's do that: as we iterate through candidate indexes i, we will maintain the correct value of leftsum.
해보자: 우리가 인덱스 i를 반복(여기서는 증가)할수록, 왼쪽 합을 계속해서 올바른 값으로 유지할 것(=피봇 인덱스를 찾았을 때 알맞은 왼쪽합을 correct value라고 칭하는 듯)이다.
[ 모범 답안 ]
public int pivotIndex(int[] nums) {
int sum = 0, leftsum = 0;
// 전체 합(S)를 구함
for (int x: nums) sum += x;
for (int i = 0; i < nums.length; ++i) {
// 왼쪽 합 == 전체 합 - 왼쪽 합 - 이번 인덱스(i) --> i 리턴
if (leftsum == sum - leftsum - nums[i]) return i;
// 아니면 그냥 계속 더하자
leftsum += nums[i];
}
return -1;
}- Time Complexity: BigO(N), where N is the length of nums.
- Space Complexity: BigO(1), the space used by leftsum and S.
1. 피봇 인덱스 같이 왼쪽, 오른쪽 합 같은게 나오면 전체 합에서 빼는 경우도 생각해보자.
2. 냅다 for loop 쓰기 전에 한 번 더 생각해보자^^
'CS 라이프' 카테고리의 다른 글
| 이번에도 힘들었던 인턴십 구하기 여정 - 합격 전 (1) | 2024.03.22 |
|---|---|
| [Teaching Assistant] 조교 일 얻기 & 학교 온보딩 프로세스 (1) | 2023.02.04 |
| [LeetCode#121] Best Time to Buy and Sell Stock (0) | 2022.11.30 |
| [OOP_Lab5] Huffman coding (recursive methods) - 1편 (0) | 2022.10.27 |
| 우당탕탕 LeetCode 스터디 그룹 결성하기 (0) | 2022.10.11 |